Learn

In this section, you can find tutorial notebooks that describe the internals of pyhgf, the theory behind the Hierarchical Gaussian filter, and step-by-step application and use cases of the model. At the beginning of every tutorial, you will find a badge to run the notebook interactively in a Google Colab session.

Theory

An introduction to the Hierarchical Gaussian Filter

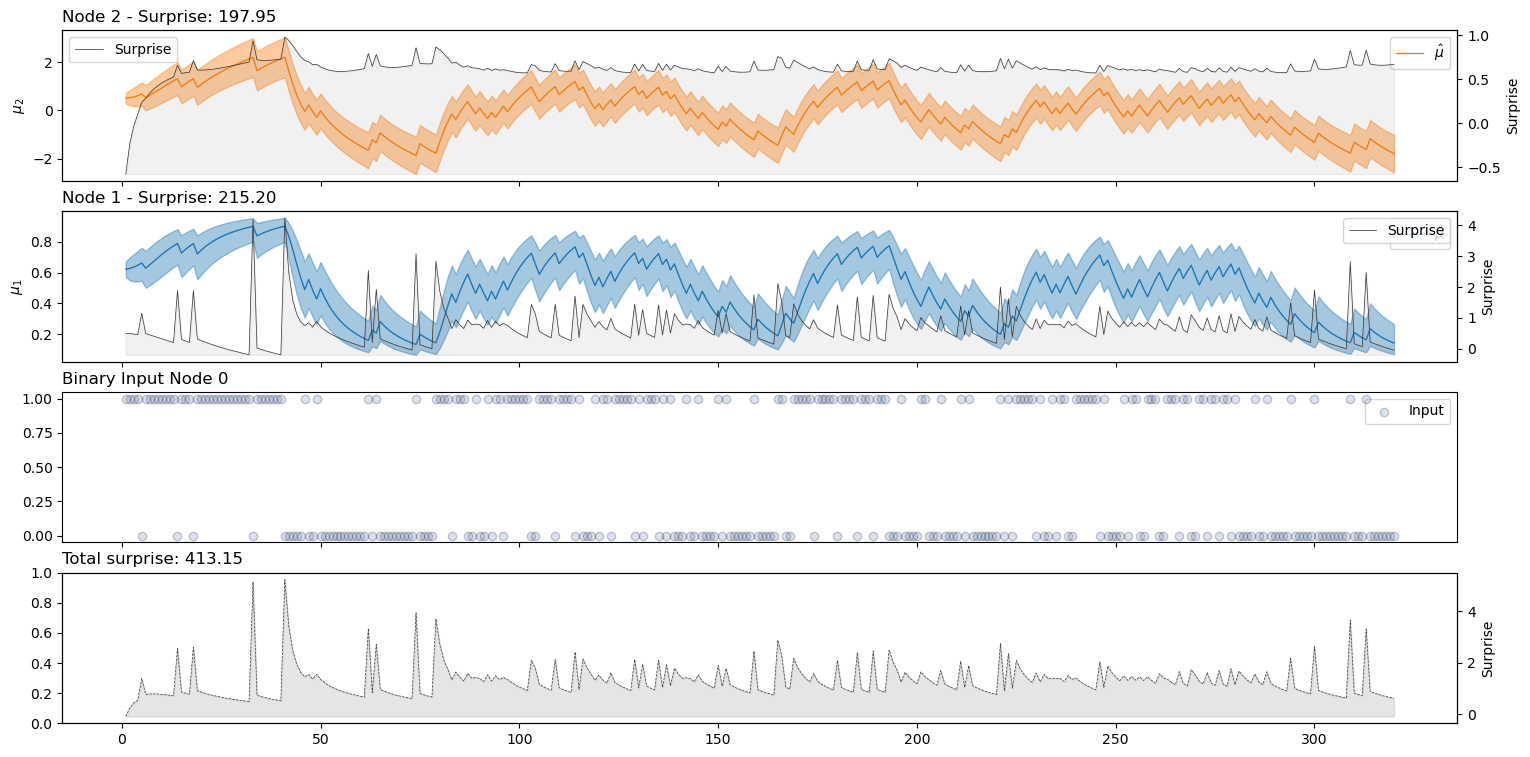
How the generative model of the Hierarchical Gaussian filter can be turned into update functions that update nodes through value and volatility coupling?

Introduction to the Generalised Hierarchical Gaussian Filter

Creating and manipulating networks of probabilistic nodes

How to create and manipulate a network of probabilistic nodes for reinforcement learning? Working at the intersection of graphs, neural networks and probabilistic frameworks.

Creating and manipulating networks of probabilistic nodes

Generalised Bayesian filtering

Predict, filter and smooth any distribution from the exponential family using generalisations of the Hierarchical Gaussian Filter.

From Reinforcement Learning to Generalised Bayesian Filtering

The Hierarchical Gaussian Filter

The binary Hierarchical Gaussian Filter

Introducing with example the binary Hierarchical Gaussian filter and its applications to reinforcement learning.

The binary Hierarchical Gaussian Filter

The categorical Hierarchical Gaussian Filter

The categorical Hierarchical Gaussian Filter is a generalisation of the binary HGF to handle categorical distribution with and without transition probabilities.

The categorical Hierarchical Gaussian Filter

The continuous Hierarchical Gaussian Filter

Introducing with example the continuous Hierarchical Gaussian filter and its applications to signal processing.

The continuous Hierarchical Gaussian Filter

Tutorials

Advanced customisation of predictive coding neural networks and Bayesian modelling for group studies.

Using custom response functions

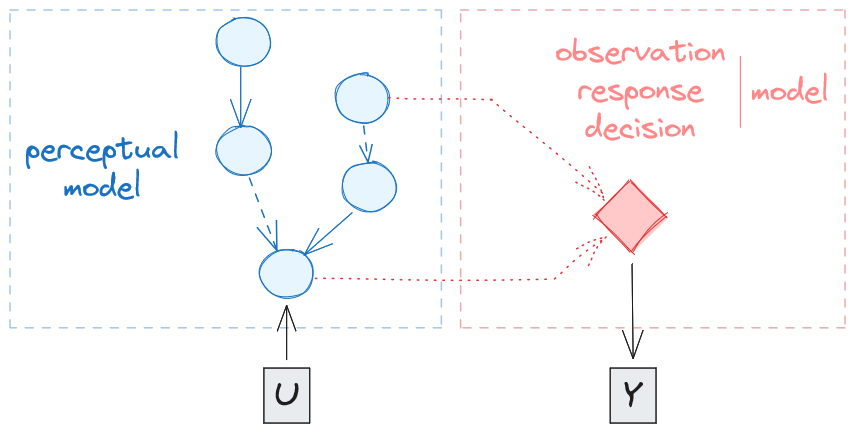
How to adapt any model to specific behaviours and experimental design by using custom response functions.

Using custom response models

Embedding the Hierarchical Gaussian Filter in a Bayesian network for multilevel inference

How to use any model as a distribution to perform hierarchical inference at the group level.

Hierarchical Bayesian modelling with probabilistic neural networks

Parameter recovery, prior and posterior predictive sampling

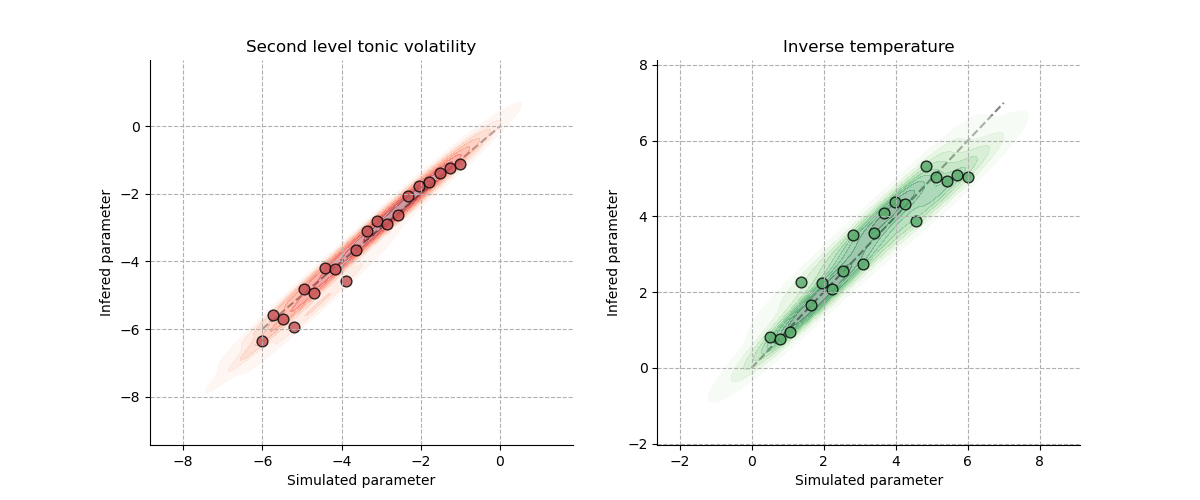
Recovering parameters from the generative model and using the sampling functionalities to estimate prior and posterior uncertainties.

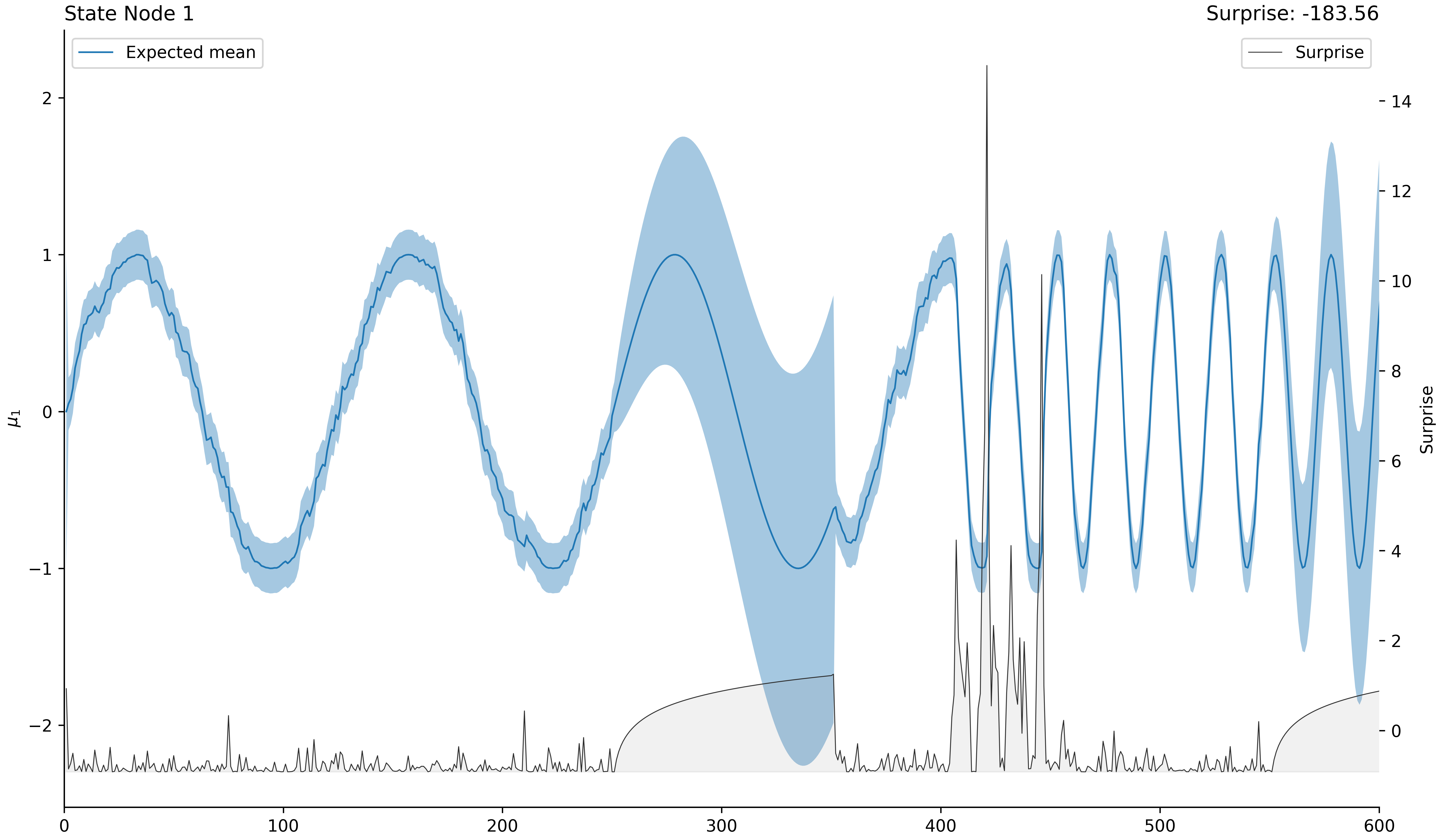
Recovering computational parameters from observed behaviours

Non-linear value coupling

Recovering parameters from the generative model and using the sampling functionalities to estimate prior and posterior uncertainties.

Non-linear value coupling between continuous state nodes

Use cases

Examples of possible applications and extensions of the standards Hierarchical Gaussian Filters to more complex experimental designs

Inferring cardiac beliefs using Bayesian filtering

Application of continuous Bayesian filtering to cardiac physiological recordings to infer interoceptive beliefs and their volatility.

Example 1: Bayesian filtering of cardiac volatility

Value and volatility coupling with an input node

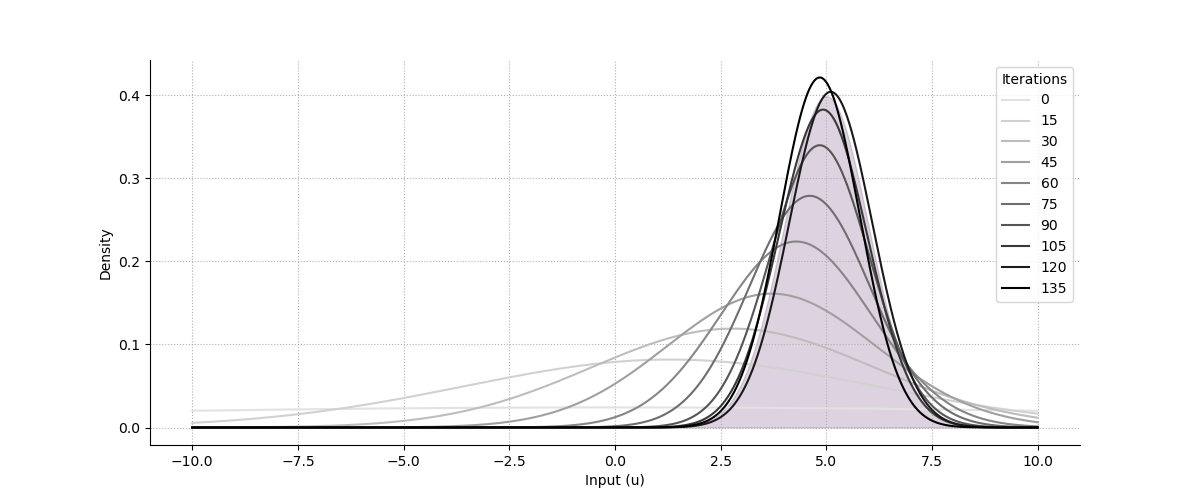
Dynamic inference over both the mean and variance of a normal distribution.

Example 2: Estimating the mean and precision of a time-varying Gaussian distributions

Multi-armed bandit task with independent reward and punishments

A generalisation of the binary Hierarchical Gaussian Filter to multiarmed bandit where the probabilities of the outcomes are evolving independently.

Example 3: A multi-armed bandit task with independent rewards and punishments

Exercises

Hand-on exercises for theComputational Psychiatry Course (Zurich) to build intuition around the generalised Hierarchical Gaussian Filter, how to create and manipulate probabilistic networks, design an agent to perform a reinforcement learning task and use MCMC sampling for parameter inference and model comparison—about 4 hours.

Introduction to the Generalised Hierarchical Gaussian Filter

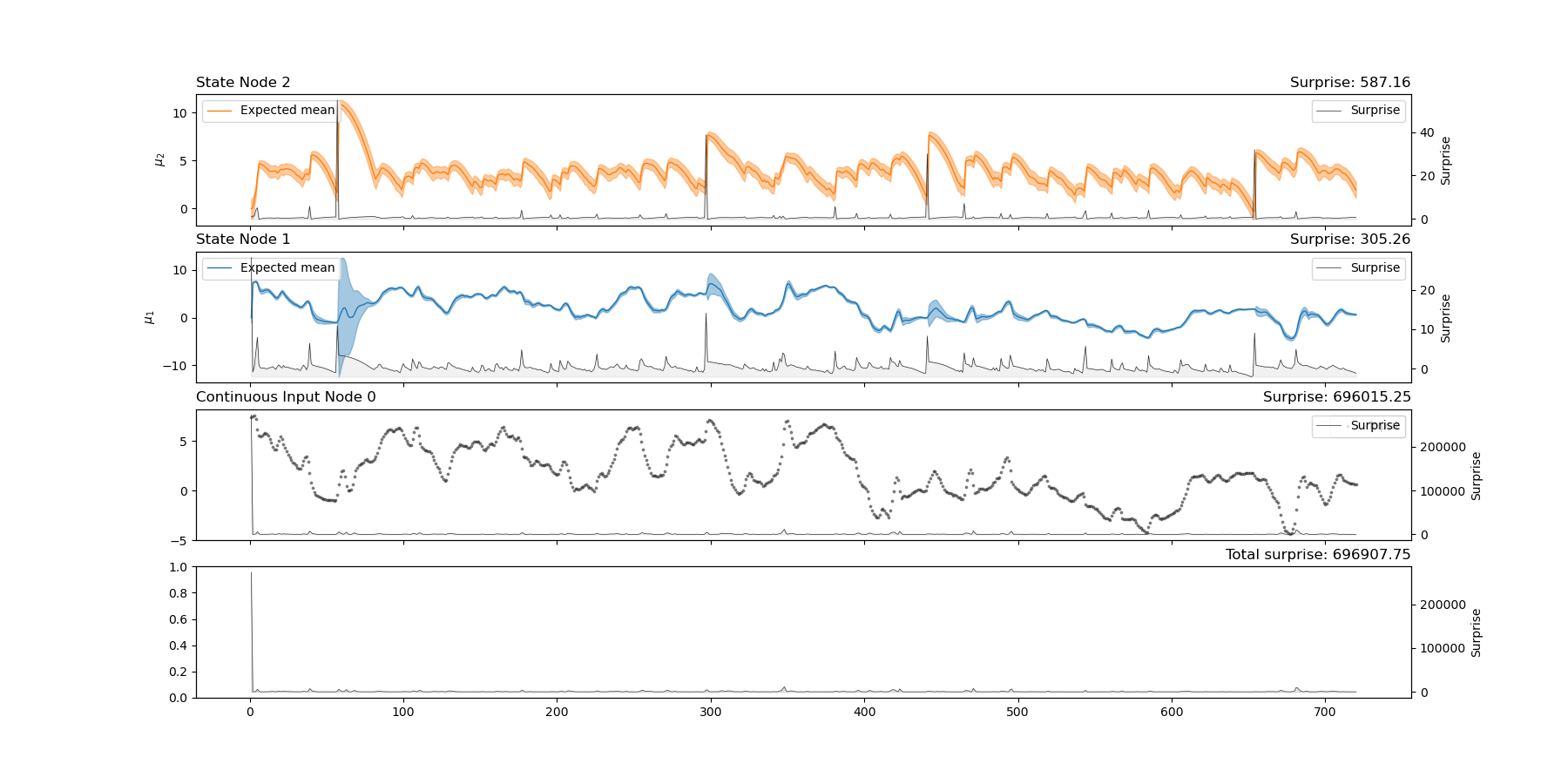
Theoretical introduction to the generative model of the generalised Hierarchical Gaussian Filter and presentation of the update functions (i.e. the first inversion of the model).

Zurich CPC I: Introduction to the Generalised Hierarchical Gaussian Filter

Applying the Hierarchical Gaussian Filter to reinforcement learning

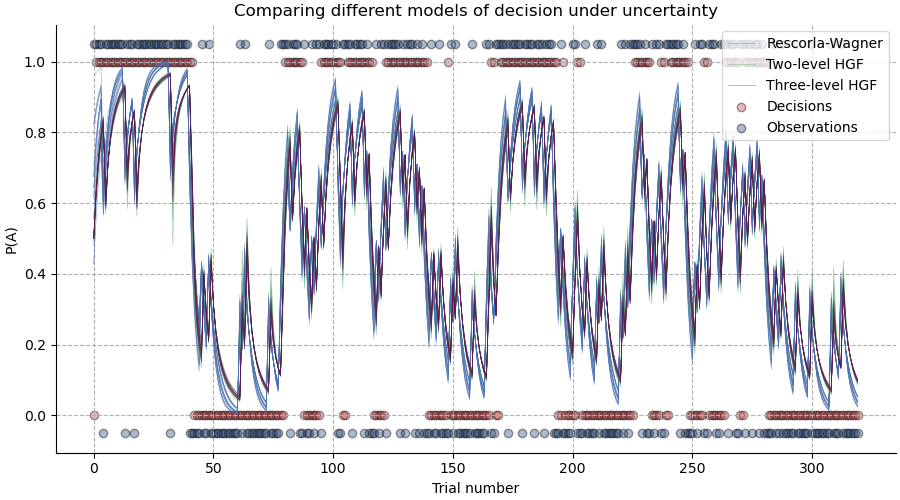
Practical application of the generalised Hierarchical Gaussian Filter to reinforcement learning problems and estimation of parameters through MCMC sampling (i.e. the second inversion of the model).

Zurich CPC II: Application to reinforcement learning